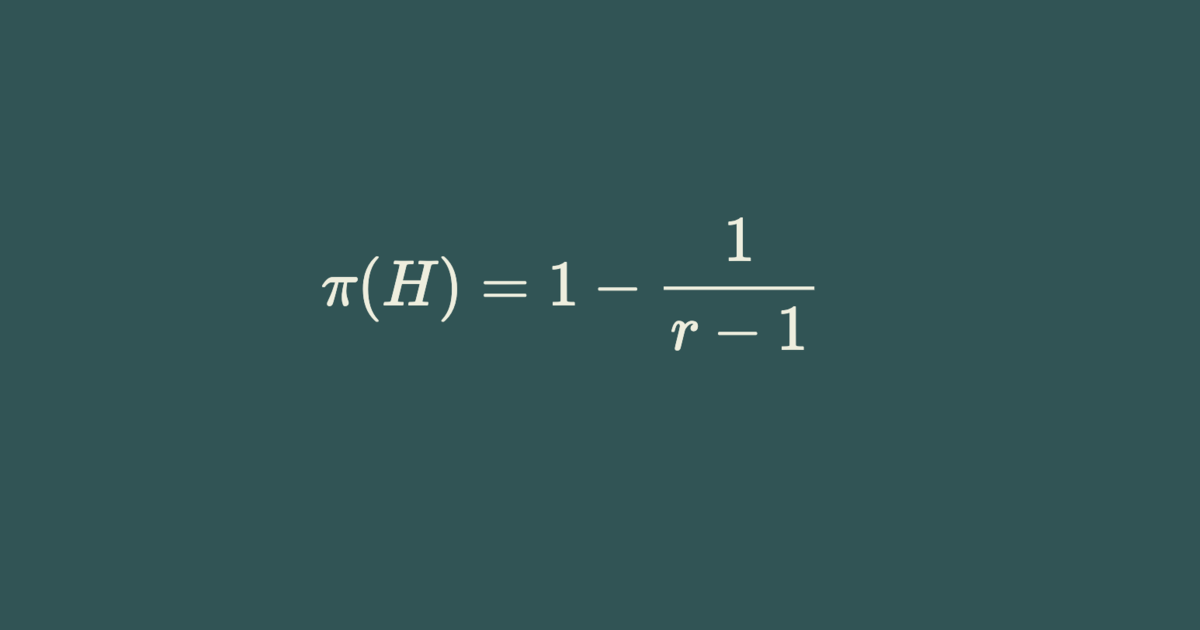Erdös–Stone Theorem
Basics
Definition 0.1 (Chromatic number) The chromatic number of a graph $G$ is defined as
\[\chi(G) = \text{min}\{k \geq 1 ~|~ G \text{ is } k \text{-colourable}\}.\]Remark:
- For $k \in \mathbb{N}$, a $k$-colouring of a graph $G$ is $c : V(G) \to [k]$, where $[k] = \{1,2,…,k\}$, such that if $vw \in E$, then $c(v) \neq c(w)$.
- A graph $G$ is said to be $k$-colourable if it has a $k$-colouring.
Definition 0.2 (Extremal number) The extremal number of a graph $H$ is defined as
\[\text{ex}(n,H) = \max\{|E(G)|: G = (V,E), |V| = n \text{ and } G \text{ is } H \text{-free}\}.\]Remark:
- Given graphs $G$ and $H$, we say that $G$ is $H$-free if $G$ does not contain a copy of $H$.
- A graph $G$ contains a copy of $H$ if $G$ has a subgraph isomorphic to $H$.
- Graphs $G$ and $H$ are isomorphic if there is a bijection $f: V(G) \to V(H)$ such that $vw \in E(G) \iff f(v)f(w) \in E(G)$.
Propostion 0.3 (Double counting principle) If $G = (A, B;E)$ is a bipartite graph, then
\[\sum_{a \in A} d(a) = \sum_{b \in B} d(b).\]Lemma 0.4 (Handshake lemma) If $G$ is a graph, then
\[\sum_{v \in V(G)} d(v) = 2|E(G)|.\]Definition 0.5 (Turán density) The Turán density of a graph $F$ is defined as
\[\pi(F) = \lim_{n \to \infty} \frac{\text{ex}(n,F)}{n \choose 2}.\]Remark:
- Determining the value of ex$(n,H)$ for a fixed graph $H$ is called the Turán problem for $H$.
Theorem 0.6 (Turán 1941) If $2 \leq r \leq n$ are integers and $G$ is $K_{r+1}$-free graph of order $n$ and size ex$(n, K_{n+1})$, then $G$ is isomorphic to $T_r(n)$.
Remark:
- The Turán graph $T_r(n)$ is defined to be the complete $r$-partite graph of order $n$ and vertex classes as equal as possible.
- It is straightforward to check that $\pi(K_{r+1}) = 1-1/r$.
Theorem 0.7 (Kövári-Sós-Turán 1954) If $n \geq r \geq s \geq 2$, then
\[\text{ex}(n, K_{r,s}) \leq \frac{1}{2} (r-1)^{\frac{1}{s}}n^{2-\frac{1}{s}} + \frac{1}{2}(s-1)n.\]Remark:
- In particular,ex$(n, K_{r,s}) = \mathcal{O}(n^{2-\frac{1}{s}})$ which implies that $\pi(K_{r,s}) = 0$.
- Note that Turán theorem gives a full answer to the Turán problem for complete graphs, but this is more difficult for bipartite graphs and we settle for upper bounds for now.
Erdös-Stone: the fundamental theorem of extremal graph theory
Turán’s theorem implies that for $r \geq 3$,
\[\pi(K_r) = 1 - \frac{1}{r-1} = 1- \frac{1}{\chi(K_r) - 1}.\]Also, Kövári-Sós-Turán theorem implies that for $r \geq s \geq 2$,
\[\pi(K_{r,s}) = 0 = 1-\frac{1}{\chi(K_{r,s}) - 1}.\]In fact, this holds in general and allow us to determine the Turán density of any graph in terms of its chromatic number.
Theorem 0.8 (Erdös-Stone 1946) If $H$ is a graph with chromatic number $\chi(H) = r$, then
\[\pi(H) = 1 - \frac{1}{r-1}.\]Outline of the proof: We prove the equality by showing $\pi(H) \geq 1 - \frac{1}{r-1}$ and $\pi(H) \leq 1 - \frac{1}{r-1}$. The former inequality is easy, but the latter is more difficult. To prove the latter inequality, we will need 2 more lemmata.
Lemma 0.9 Let $0 < c, \epsilon < 1$ and $n > 2(1+1/c)/\epsilon$. If $G$ is a graph of order $n$ with at least $(c+\epsilon){n \choose 2}$ edges, then $G$ contains a subgraph $G’$ of order $n’ \geq \epsilon^{1/2}n$ with minimum degree $\delta(G’) \geq cn’$.
Remark: It is essentially saying that any graph $G$ conatins a large subgraph with minimum degree close to the average degree of $G$.
Proof of lemma 0.9 (Algorithmic and contradictory). Step 1: Set $G_n = G$. If $\delta(G_n) \geq cn$, then set $G’= G$ and we are done. Otherwise, there exists $v_n \in V(G_n)$ such that $d(v_n) < cn$. Remove this vertex $v_n$ to give a subgraph $G_{n-1}$ of order $n-1$. Step 2: If $\delta(G_{n-1}) \geq c(n-1)$, then let $G’ = G_{n-1}$. Otherwise, there exists $v_{n-1} \in V(G_{n-1})$ such that $d(v_{n-1}) < c(n-1)$. Remove this vertex $v_{n-1}$ to give a subgraph $G_{n-2}$ of order $n-2$. Coninue this process to construct a sequence of subgraphs of $G$: $G_n, G_{n-1}, \cdots, G_k, G_{k-1}, \cdots$, where $G_k$ has order $k$ and $G_{k-1}$ is obtained from $G_k$ by removing vertex $v_{k}$ in $G_k$ with $d(v_k) < ck$.
Claim: The above process must terminate at some $k > s := \lceil \epsilon^{1/2}n\rceil$, yielding $G’ = G_k$ of order $k$ with minimum degree at least $ck$. To complete the proof of lemma 0.9, it remains to prove this claim. Suppose, for the sake of contradiction, that this process terminate at some $k \leq s$. The number of edges removed at step $n+1-i$ is at most $ci$. Hence, we have
\[\begin{align} |E(G_s)| &> |E(G)| - \sum_{k = s+1}^n ck\\ & \geq (c+\epsilon){n \choose 2} - c\left({n \choose 2} + n - {s+1 \choose 2}\right)\\ & \geq \epsilon {n \choose 2} - cn + c{s+1 \choose 2}\\ & > \epsilon {n \choose 2} + n\\ & = \frac{\epsilon n^2 + n(2 - \epsilon)}{2}\\ & > \frac{\epsilon n^2 - \epsilon^{1/2}n}{2}\\ \end{align}\](2) \(\sum_{k = s+1}^n k = {n+1 \choose 2} - {s+1 \choose 2} = {n \choose 2} + n - {s+1 \choose 2}.\)
(4) As $s = \lceil \epsilon^{1/2}n\rceil$ and $n > 2(1+1/c)/\epsilon$ by the assumption, we have
- (6) We have $0< \epsilon < 1$.
We have shown that $|{E(G_s)}| > {n \choose 2}$, meaning that $G_s$ contains an impossibly large number of edges. This is a contradiction, and the claim is proven. ◼
Lemma 1.0 Let $r \geq 2$, $t \geq 1$, and $0 < \epsilon < 1/r$. There exists $n_0(r,t,\epsilon)$ such that if $G$ is of order $n \geq n_0$ with minimum degree $\delta(G) \geq (1-\frac{1}{r-1} + \epsilon)n$, then $G$ contains a copy of $K_r(t)$, where $K_r(t)$ is the complete $r$-partite graph with $t$-vertices in each class.
Remark: It is essentially saying that any graph with sufficiently large minimum degree and order must contain a copy of $K_r(t)$.
Proof of lemma 1.0 (Induction). The base case $r = 2$ follows from theorem 0.7. Notice that $K_2(t) = K_{t,t}$ and
\(\text{ex}(n, K_{t,t}) \leq \frac{1}{2}(t-1)^{1/t}n^{2-1/t} + \frac{1}{2}(t-1)n < tn^{2-1/t}.\) Given $0 < \epsilon_0 < 1/2$ and $t \geq 1$, let $n_0(2,t,\epsilon_0) = (2t/\epsilon_0)^t$, then for $n \geq n_0(2,t,\epsilon_0)$, we have $\epsilon_0 \geq 2t/n^{1/t}$. Let $G$ be a graph of order $n \geq n_0(2,t,\epsilon_0)$ and $\delta(G) \geq \epsilon_0n$, then by lemma 0.4,
\[|E(G)| \geq \frac{\epsilon_0n^2}{2} \geq tn^{2-1/s} > \text{ex}(n, K_{t,t}),\]so $G$ contains a copy of $K_2(t)$.
Suppose that $r \geq 3$ and the result holds for $r-1$. Let $t \geq 1$ and $0 < \epsilon< 1/r$. Let $G$ have order $n$ and $\delta(G) \geq (1-\frac{1}{r-1}+\epsilon)n$. We want to show that if $n$ is sufficiently large, then $G$ contains a copy of $K_r(t)$. We do this by using our inductive hypothesis to find a complete $(r-1)$-partite graph in $G$ with large vertex classes.
Let $w = \lceil 2t/\epsilon \rceil > t$ and $n_0(r-1, w, \epsilon)$, where the existence of $n_0(r-1, w, \epsilon)$ is from our inductive hypothesis. Since $1-\frac{1}{r-1}+\epsilon > 1-\frac{1}{r-2}+\epsilon$, our inductive hypothesis guarantees that $G$ contains a copy H of $K_{r-1}(w)$. Let
\(V(H) = W = W_1 \cup W_2 \cup \cdots \cup W_{r-1},\) be the vertex partition (so $W_i$’s are pairwise disjoint) of $H$, with $|W_i| = w$ for $i \leq i \leq r-1$. Now we use $H$ to help us to find a copy of $K_r(t)$ in $G$, since any choice of $t$ vertices from each $W_i$ gives us a copy of $K_{r-1}(t)$. So we have lots of copies of $K_{r-1}(t)$, but how can we extend one of them to give a copy of $K_r(t)$? Short answer: We identify a set of vertices that are not in $V(H)$ but have lots of neighbours in $V(H)$, which could potentially be used to build a copy of $K_r(t)$ from one of the many copies of $K_{r-1}(t)$ in $H$.
Let $S = \{v \in V\setminus W \ : v \text{ has } \geq (r-2)w + t \text{ neighbours in }H\}$. There are in total $(r-1)w$ vertices in $H$, so each $v \in S$ has at least $t$ neighbours in each class $W_i$. Suppose, for the sake of contradiction, that $G$ is $K_r(t)$-free. We say that a vertex $v \in S$ covers a copy $L$ of $K_{r-1}(t)$ contained in $H$ if $v$ is adjacent to every vertex in $L$, and that $(v, L)$ is a covering pair if $v \in S$ and $L$ is a copy of $K_{r-1}(t)$ in $H$ that is covered by $v$. This is a double counting argument, since we can form a new graph $F(S, D; T)$, where $D$ is the set of all copies of $K_{r-1}(t)$ in $H$, and if $x \in S$ and $Y \in D$, then $xy \in T \iff (x,Y)$ is a covering pair. Also, note that no copy of $K_{r-1}(t)$ in $H$ is covered by more that $t-1$ vertices from $S$ as $G$ is $K_r(t)$-free. Thus,
\[|S| \leq \sum_{x \in S}d_F(x) = \sum_{Y \in D}d_F(Y) \leq (t-1)|D| = (t-1){w \choose t}^{r-1}.\]Then the contradiction comes from the following claim. But before that, let’s see a diagram of the graph $G$. If we define $A = \{v \in V\setminus W \ : v \text{ has } < (r-2)w + t \text{ neighbours in }H\}$, then the graph looks something like this. 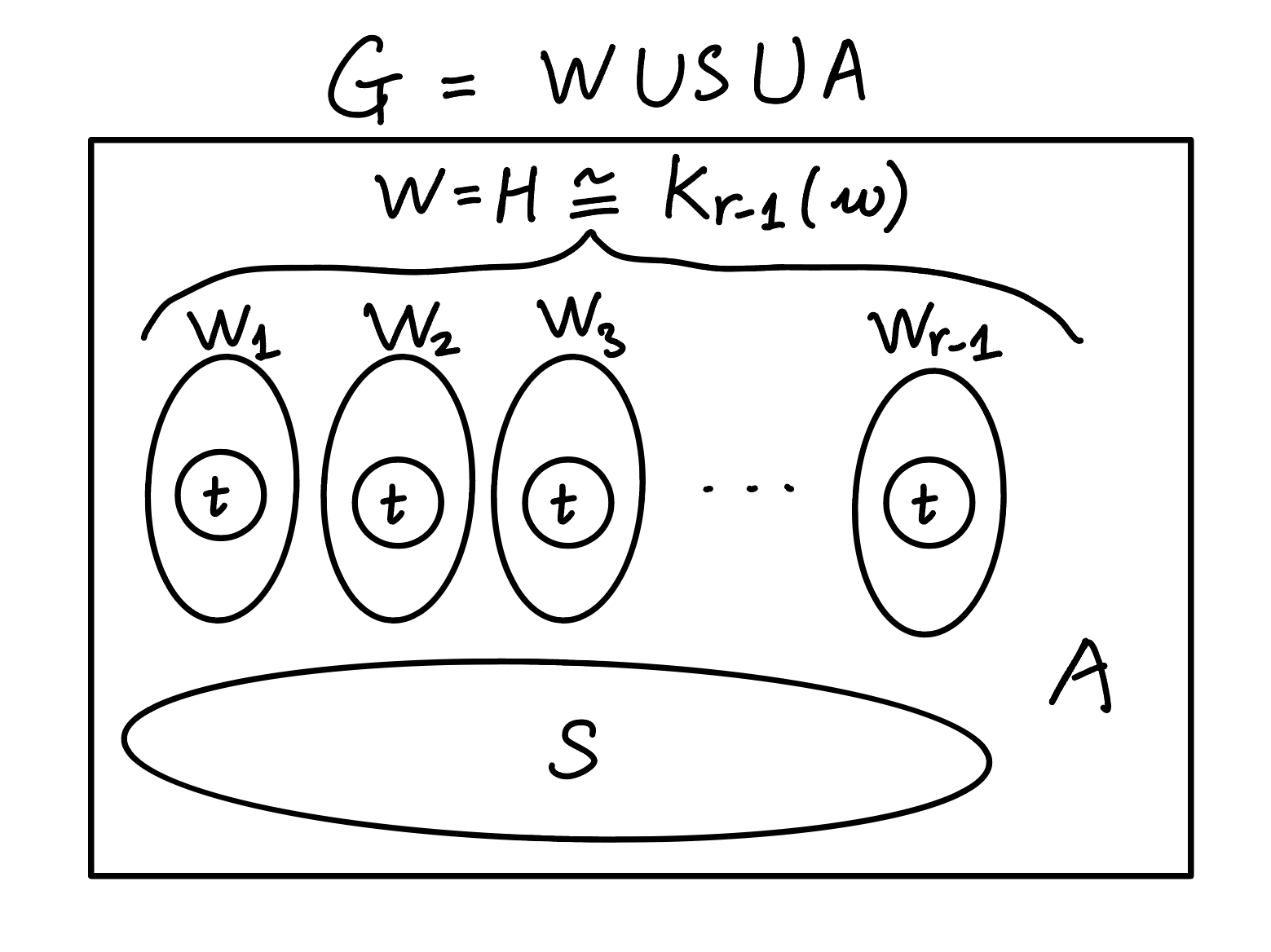 A diagram of graph G
A diagram of graph G
Claim: For $n$ sufficiently large, we have $|S| > (t-1){w \choose t}^{r-1}$.
Proof of the claim: Estimate the number of edges between $W$ and $V\setminus W$, which we denote by $e(W, V \setminus W)$.
We first consider the lower bound for $e(W, V \setminus W)$. We have $\delta(H) \geq (1-\frac{1}{r-1}+\epsilon)n$ since $\delta(G) \geq (1-\frac{1}{r-1}+\epsilon)$ and $H$ is a subgraph of $G$. Moreover, the number of edges inside $W$, denoted by $e(W)$ is at most ${|W| \choose 2} < |W|^2/2$, hence
\[\begin{align} e(W, V \setminus W) = \sum_{v \in W}\left(d(v) - 2e(W) \right) > |W|n(1-\frac{1}{r-1}+\epsilon) - |W|^2. \end{align}\]Next we consider the upper bound for $e(W, V \setminus W)$. If $v \in A$, then $v$ has less than $(r-2)w = t$ neighbours in $W$. If $v \in S$, then $v$ has less than $|W|$ neighbours in $W$. Using these bounds and the fact that $|W| = (r-1)w$, we have
\[\begin{align} e(W, V \setminus W) &< ((r-2)w+t)(n - |W| - |s|) + |W||S|\\ & = n((r-2)w+t)+|S|(w-t)-|W|^2+|W|(w-t). \end{align}\]Combining (7) and (9) and simplifying, we have
\[\begin{align*} |W|n(1-\frac{1}{r-1}+\epsilon) - |W|^2 &< n((r-2)w+t)+|S|(w-t)-|W|^2+|W|(w-t)\\ \implies |W|n - wn + n\epsilon(r-1)w &< n(|W| - w + t) + |S|(w-t) + |W|(w-t)\\ \implies n(\epsilon(r-1)w-t) &< |S|(w-t) + (r-1)w(w-t)\\ \implies |S| &> n\left(\frac{\epsilon(r-1)w - t}{w-t} - (r-1)w\right). \end{align*}\]As $w \geq 2t/\epsilon$, we have $|S| = \mathcal{O}(n)$, and hence $|S| \to \infty$ as $n \to \infty$. For sufficiently large $n$, $|S| > (t-1){w \choose t}^{r-1}$ as required, which completes the proof of the claim and hence this lemma. ◼
Now we have everything we need to prove the Erdös–Stone Theorem.
Proof of theorem 0.8. If $H$ is a graph with $\chi(H) = r \geq 2$, then $T_{r-1}(n)$ is $H$-free since $\chi(T_{r-1}) = r - 1$. Then, by Turán’s theorem,
\[\text{ex}(n,H) \geq |E(T_{r-1}(n))| = \text{ex}(n,K_r),\]so
\[\pi(H) \geq \pi(K_r) = 1 - \frac{1}{r-1}.\]Let’s consider the reverse inequality. If $\chi(H) = r$, then $H$ is a subgraph of $K_r(t)$ for any $t \geq |V(H)|$. So a graph that is $H$-free is also $K_r(t)$-free for large enough $t$ and hence $\pi(H) \geq \pi(K_r(t))$ (why?:) for large enough $t$. Now it it remained to show that
\[\begin{align} \pi(K_r(t)) \leq 1 -\frac{1}{r-1}. \end{align}\]Suppose, for the sake of contradiction, that (10) fails to hold. Then $\exists \epsilon’$ such that
\[\pi(K_r(t)) > 1- \frac{1}{r-1} + 3\epsilon'.\]By the definition of limits, for sufficiently large $n$, we have
\[\begin{align} \text{ex}(n, K_r(t)) > (1-\frac{1}{r-1} + 2\epsilon'){n \choose 2}. \end{align}\]Let $n \geq n_0(r,t,\epsilon’)/\sqrt{\epsilon’}$, where $n_0(r,t,\epsilon’)$ is defined by lemma 1.0, and $G$ be a $K_r(t)$-free graph of order $n$ and at least of size $(1-\frac{1}{r-1} + 2\epsilon’){n \choose 2}$, which exists by (11). By lemma 0.9, $G$ contains a subgraph $G’$ of order $n’ \geq \sqrt{\epsilon’}n \geq n_0(r,t,\epsilon’)$ and with minimum degree $\delta(G’) \geq (1 - \frac{1}{r-1} + \epsilon’)n’$ by noting that $c = \epsilon’$. Finally, by lemma 1.0, $G’$ contains a copy of $K_r(t)$, and $G$ is not $K_r(t)$-free.
This contradiction completes the proof of theorem 0.8. ◼