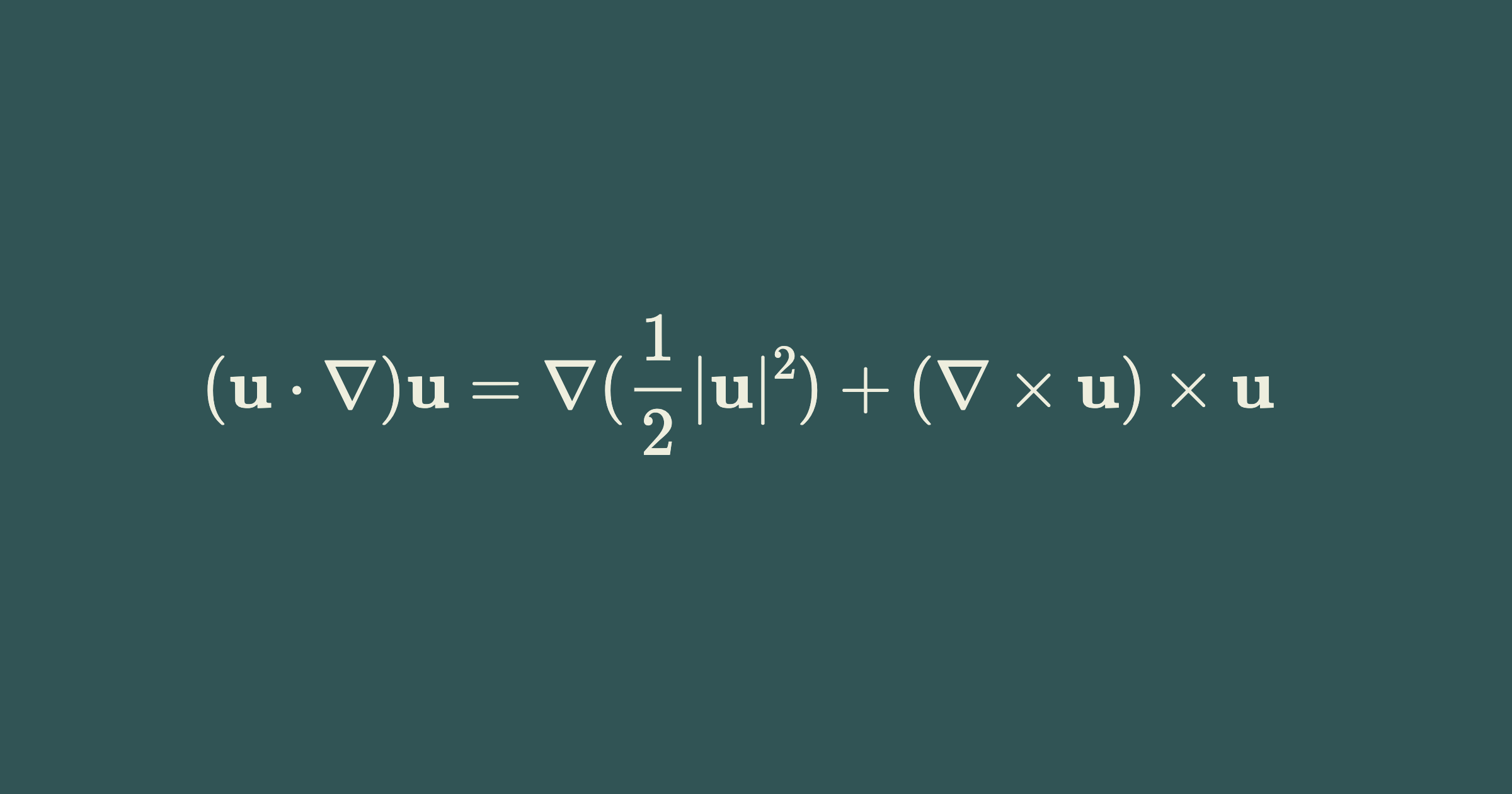Vector Identities

Introduction

In this post, we look at identities built from vector operators. These operators behave both as vectors and as differential operators, so that the usual rules of taking the derivative of, say, a product must be observed. In particular, we will use the Einstein summation convention in the proof.

Basics

Recall that

\[\begin{align*} &\textbf{a} \cdot \textbf{b} = a_ib_i,\\ &\textbf{a} \times \textbf{b} = \epsilon_{ijk}a_ib_j\mathbf{e}_k,\\ &\nabla = \frac{\partial \mathbf{e}_i}{\partial x_i}, \:\text{(differential operator)}\\ &\nabla \cdot \mathbf{a} = \frac{\partial a_i}{\partial x_i},\:\text{(divergence of $\mathbf{a}$)}\\ &\nabla \times \mathbf{a} = \epsilon_{ijk}\frac{\partial a_j}{\partial x_i}\mathbf{e}_k,\:\text{(curl of $\mathbf{a}$)}\\ &\nabla \phi = \frac{\partial \phi}{\partial x_i}\mathbf{e}_i, \:\text{(gradient of $\mathbf{a}$)}\\ &\epsilon_{ijk}\epsilon_{imn}=\delta_{jm}\delta_{kn}-\delta_{jn}\delta_{km}. \end{align*}\]

Identity 1.

\[\nabla \cdot (\nabla \times \textbf{a})=0\]

Proof:

\[\begin{align*} \nabla \cdot (\nabla \times \textbf{a}) &= \frac{\partial}{\partial x_i}(\nabla \times \textbf{a})\\ &=\frac{\partial}{\partial x_i}\left(\epsilon_{ijk} \frac{\partial a_k}{\partial x_j}\right)\\ &=\epsilon_{ijk} \frac{\partial^2 a_k}{\partial x_i \partial x_j}\\ &=\epsilon_{jik} \frac{\partial^2 a_k}{\partial x_j \partial x_i} ~~~~~~~\text{relabel indices i.e. $i \to j,\: j\to i$}\\ &=\epsilon_{jik} \frac{\partial^2 a_k}{\partial x_i \partial x_j} ~~~~~~~\text{swap order of differentiation}\\ &=-\epsilon_{jik} \frac{\partial^2 a_k}{\partial x_i \partial x_j}=0 ~~~~~~~\text{swap indices in permutation}\\ \end{align*}\]

Identity 2.

\[\nabla \times (\nabla \phi )=\textbf{0}\]

Proof:

\[\begin{align*} \nabla \times (\nabla \phi) &=\nabla \times \frac{\partial \phi}{\partial x_m}\mathbf{e}_m\\ &=\epsilon_{ijk}\frac{\partial}{\partial x_i}\left(\frac{\partial \phi}{\partial x_j}\right)\mathbf{e}_k\\ &=\epsilon_{ijk} \frac{\partial^2 \phi}{\partial x_i \partial x_j} \mathbf{e}_k\\ &=\epsilon_{jik} \frac{\partial^2 \phi}{\partial x_j \partial x_i}\mathbf{e}_k ~~~~~~~\text{relabel indices i.e. $i \to j,\: j\to i$}\\ &=\epsilon_{jik} \frac{\partial^2 \phi}{\partial x_i \partial x_j}\mathbf{e}_k ~~~~~~~\text{swap order of differentiation}\\ &=-\epsilon_{ijk} \frac{\partial^2 \phi}{\partial x_i \partial x_j}\mathbf{e}_k=\mathbf{0} ~~~~~~~\text{swap indices in permutation}\\ \end{align*}\]

Identity 3.

\[\nabla \cdot (\phi \textbf{a})= (\mathbf{a} \cdot \nabla \phi) + \phi (\nabla \cdot \mathbf{a})\]

Proof:

\[\begin{align*} \nabla \cdot (\phi \textbf{a}) &= \frac{\partial (\phi \mathbf{a})_i }{\partial x_i}\\ &=\frac{\partial (\phi a_i) }{\partial x_i}\\ &=a_i \frac{\partial \phi}{\partial x_i} + \phi \frac{\partial a_i}{\partial x_i}~~~~~~~\text{product rule of differentiation}\\ &=a_i(\nabla \phi)_i + \phi (\nabla \cdot \mathbf{a})\\ &=(\mathbf{a} \cdot \nabla \phi) + \phi (\nabla \cdot \mathbf{a})\\ \end{align*}\]

Identity 4.

\[\nabla \times (\phi \textbf{a})= \phi(\nabla \times \textbf{a})+\textbf{a} \times \nabla \phi\]

Proof:

\[\begin{align*} \nabla \times (\phi \textbf{a}) &= \epsilon_{ijk} \frac{\partial (\phi \mathbf{a})_j}{\partial x_i} \mathbf{e}_k\\ &=\epsilon_{ijk} \frac{\partial (\phi a_j)}{\partial x_i} \mathbf{e}_k\\ &= \epsilon_{ijk} \left(\frac{\partial \phi}{\partial x_i}a_j+\frac{\partial a_j}{\partial x_i} \phi \right) \mathbf{e}_k~~~~~~~\text{ product rule of differentiation}\\ &=\epsilon_{ijk}a_j \frac{\partial \phi}{\partial x_i}\mathbf{e}_k + \epsilon_{ijk} \phi \frac{\partial a_j}{\partial x_i} \mathbf{e}_k\\ &=(\nabla \phi \times \mathbf{a})+(\nabla \times \mathbf{a})\phi \end{align*}\]

Identity 5.

\[\nabla \times (\textbf{a} \times \textbf{b}) = \textbf{a}(\nabla \cdot \textbf{b}) + [\textbf{b} \cdot \nabla] \textbf{a} + [\textbf{a} \cdot \nabla]\textbf{b} - \textbf{b}(\nabla \cdot \textbf{a})\]

Proof:

\[\begin{align*} \nabla \times (\textbf{a} \times \textbf{b}) &= \nabla \times (\epsilon_{ijk} a_i b_j \mathbf{e}_k)\\ &=\nabla \times (d_k \mathbf{e}_k) ~~~~~~~\text{where }d_k=\epsilon_{ijk}a_ib_j\\ &=\epsilon_{lmn} \frac{\partial d_m}{\partial x_l} \mathbf{e}_n\\ &=\epsilon_{lmn}\epsilon_{ijk}\frac{\partial (a_i b_j)}{\partial x_l} \mathbf{e}_n\\ &=(\delta_{ni}\delta_{lj}-\delta_{nj}\delta_{li}) \frac{\partial(a_ib_j)}{\partial x_l}\mathbf{e}_n\\ &=(\delta_{ni}\delta_{lj})\frac{\partial(a_ib_j)}{\partial x_l}\mathbf{e}_n-(\delta_{nj}\delta_{li})\frac{\partial(a_ib_j)}{\partial x_l}\mathbf{e}_n\\ &=\frac{\partial (a_nb_l)}{\partial x_l}\mathbf{e}_n-\frac{\partial (a_lb_n)}{\partial x_l}\mathbf{e}_n\\ &=(a_n\frac{\partial b_l}{\partial x_l}+b_l\frac{\partial a_n}{\partial x_l})\mathbf{e}_n-(a_l\frac{\partial b_n}{\partial x_l}+b_n\frac{\partial a_l}{\partial x_l})\mathbf{e}_n\\ &=\mathbf{a}(\nabla \cdot \mathbf{b})+[\mathbf{b} \cdot \nabla]\mathbf{a}-[\mathbf{a} \cdot \nabla]\mathbf{b}-\mathbf{b}(\nabla \cdot \mathbf{a}) \end{align*}\]

Identity 6.

\[\nabla \times (\nabla \times \textbf{a})=\nabla(\nabla \cdot \textbf{a})-\nabla^2\textbf{a}\]

Proof:

\[\begin{align*} \nabla \times (\nabla \times \textbf{a})&=\nabla \times (\epsilon_{ijk}\frac{\partial a_j}{\partial x_i}\mathbf{e}_k)\\ &=\epsilon_{lmn}\frac{\partial d_m}{\partial x_l}\mathbf{e}_n ~~~~~~~\text{where }d_k=\epsilon_{ijk}\frac{\partial a_j}{\partial x_i}\\ &=\epsilon_{lmn}\epsilon_{ijm}\frac{\partial^2 a_j}{\partial x_l \partial x_i}\mathbf{e}_n\\ &=(\delta_{ni}\delta_{lj}-\delta_{nj}\delta_{li})\frac{\partial^2 a_j}{\partial x_l \partial x_i}\mathbf{e}_n\\ &=(\delta_{ni}\delta_{lj})\frac{\partial^2 a_j}{\partial x_l \partial x_i}\mathbf{e}_n-(\delta_{nj}\delta_{li})\frac{\partial^2 a_j}{\partial x_l \partial x_i}\mathbf{e}_n\\ &=\frac{\partial^2a_l}{\partial x_l \partial x_n}\mathbf{e}_n-\frac{\partial^2a_n}{\partial x_l \partial x_l}\mathbf{e}_n\\ &=\nabla(\nabla \cdot \mathbf{a})-\nabla^2\mathbf{a} \end{align*}\]

Identity 7.

\[(\mathbf{u} \cdot \nabla) \mathbf{u} = \nabla (\frac{1}{2} |\mathbf{u}|^2) + (\nabla \times \mathbf{u}) \times \mathbf{u}\]

Proof:

\[\begin{align*} (\nabla \times \mathbf{u}) \times \mathbf{u} &= (\epsilon_{ijk} \frac{\partial u_j}{\partial x_i} \mathbf{e}_k) \times \mathbf{u}\\ & = (d_k \mathbf{e}_k) \times \mathbf{u} ~~~~~~~~\text{ where } d_k = \epsilon_{ijk} \frac{\partial u_j}{\partial x_i}\\ & = \epsilon_{lmn} d_l u_m\mathbf{e}_n\\ & = \epsilon_{lmn} \epsilon_{lij} \frac{\partial u_j}{\partial x_i} \mathbf{e}_n\\ & = (\delta_{mi} \delta_{nj} - \delta_{mj} \delta_{ni}) u_m \frac{\partial u_j}{\partial x_i} \mathbf{e}_n\\ & = u_i \frac{\partial u_j}{\partial x_i} \mathbf{e}_j - u_j \frac{\partial u_j}{\partial x_i} \mathbf{e}_i\\ & = [u_i \frac{\partial}{\partial x_i}] (u_j \mathbf{e}_j) - u_j \frac{\partial u_j}{\partial x_i} \mathbf{e}_i\\ & = [\mathbf{u} \cdot \nabla] \mathbf{u} - \nabla (\frac{1}{2} |\mathbf{u}|^2) \end{align*}\]

The notation $[\mathbf{a} \cdot \nabla]$ is called the scalar differential operator

\[[\mathbf{a} \cdot \nabla] \equiv \left[a_x \frac{\partial}{\partial x} + a_y \frac{\partial}{\partial y} + a_z \frac{\partial}{\partial z}\right].\]

• Notice that the components of $\mathbf{a}$ don’t get touched by the differentiation.
• Applied to a scalar field, results in a scalar field.
• Applied to a vector field, results in a vector field.
• The material derivative involves this operation as the acceleration due to position change.