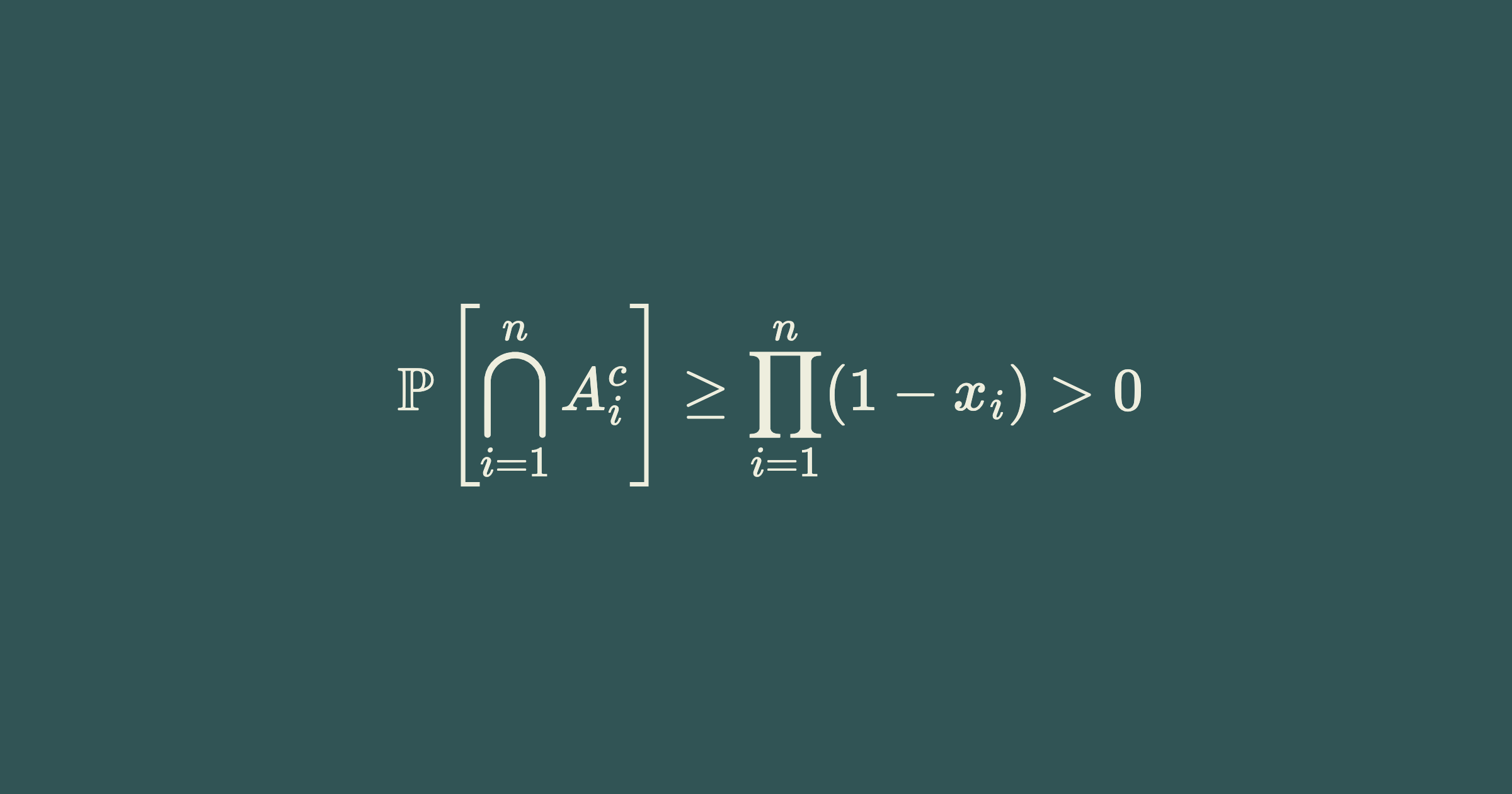The Lovász Local Lemma
Motivation
Recently, I came across an interesting application of the Lovász Local Lemma, a fundamental technique in the “probabilistic method” and a classic example of a non-constructive approach in combinatorics. Often in applying the probabilistic method, one is trying to show that it is possible to avoid “bad events” $A_1, …, A_n$ with positive probability, or in other words,
\[\begin{equation} \tag{*} \mathbb{P}\left[\bigcap_{i=1}^nA_i^c\right] > 0, \end{equation}\]where $\Omega$ is a prbability space and $A_i \subseteq \Omega$ and $A_i^c = \Omega \setminus A_i$.
The Lovász Local Lemma, to some extent, resides at the intersection of two contrasting scenarios:
If $\sum_{i = 1} \mathbb{P}[A_i]<1$, then (*) can be easily derived using the union bound.
If we have an arbitrary number of mutually independent events $(A_i)_{i = 1}^n$ and $\mathbb{P}[A_i] < 1~\forall i$, then (*) holds.
The local lemma deals with the case when each bad event is independent with most other bad events, but possibly dependent with a small number $d$ of other events.
Basics
Here are some basic definitions.
Definition 0.1 (Probability Space) A probability space is a pair $(\Omega, \mathbb{P})$, where $\Omega$ is a finite set of elementary events (e.g. {Heads, Tails} or {1,2,3,4,5,6}) and $\mathbb{P}:\Omega \to [0,1]$ such that $\mathbb{P}[\emptyset] = 0$ and $\sum_{\omega \in \Omega} \mathbb{P}[\omega] = 1$.
Definition 0.2 (Event) Any subset $A \subseteq \Omega$ is called an event and we define its probability to be $\mathbb{P}[A] = \sum_{\omega \in A}\mathbb{P}[\omega]$.
Lemma 0.3 (The Probabilistic Method) If $(\Omega, \mathbb{P})$ is a probability space and $A⊆\Omega$ is an event satisfying $\mathbb{P}[A]>0$ then $A \ne ∅$.
Proof: (Contrapositive) If $A=∅$, then $\mathbb{P}[A]=0$. ◼
Lemma 0.4 (The union bound) Let $(\Omega, \mathbb{P})$ be a finite probability space and $A_1, …, A_n \subseteq \Omega$, then
\[\mathbb{P}\left[\bigcup^{n}_{i = 1}A_i\right] \leq \sum_{i = 1}^n \mathbb{P}[A_i].\]Proof: Let $A = \cup_{i = 1}^nA_i$ and $\omega \in A$. Then $\omega \in A_i$ for some $1 \leq i \leq n$. Define $f:\Omega \to \mathbb{N}$ by $f(\omega) = \left|\{i : \omega \in A_i\}\right|$. We have $f(\omega) \geq 1 ~\forall \omega \in A$ and hence
\[\mathbb{P}\left[\bigcup_{i = 1}^n A_i\right] = \sum_{\omega \in A} \mathbb{P}[\omega] \leq \sum_{\omega \in A} f(\omega)\mathbb{P}[\omega] = \sum_{i=1}^n \mathbb{P}[A_i],\]which completes the proof. ◼
Proof of Lovász Local Lemma
The symmetric version is stated as follows:
Lemma 0.5 (Symmetric Lovász Local Lemma) Let $p \in (0,1)$ and $d \in \mathbb{N}$. Let $A_1,…, A_n$ be a sequence of events such that $\mathbb{P}[A_i] \leq p$ for all $i$, and each event is independent of all except $d$ of the others. If $\text{e}p(d + 1) \leq 1$, where $\text{e}=2.71828…$ is Euler’s number, then $\mathbb{P}[A_1^c\cap A_2^c \cap … \cap A_n^c] > 0$.
Remark: $d$ is sometimes called the “dependence degree”.
Proof strategy: We show a stronger, “asymmetric” version, and use it to prove the symmetric version.
Asymmetric Lováz Local Lemma: statement and proof
Here is a useful definition we need.
Definition 0.6 (Dependency Graph) For all integers $n > 0$, define $[n]:=\{1, …, n\}$. A graph $G = (V, E)$ is a dependency graph on events $A_1, …, A_n$ if $V = [n]$ and each event $A_i$ is mutually independent of its non-neighbours $\{A_j: j \ne i, \{i, j\} \notin E\}$.
We now state the asymmetric Lováz Local Lemma.
Lemma 0.7 (Asymmetric Lováz Local Lemma) Suppose $G$ is a dependecy graph for events $A_1, …,A_n$ and $\exists~x_1, …, x_n \in (0,1)$ such that
\[\begin{equation} \mathbb{P}[A_i] \leq x_i \prod_{\{i,j\} \in E}(1-x_j), ~~~\forall i \in [n]. \end{equation}\]Then
\[\begin{equation} \mathbb{P}\left[\bigcap_{i=1}^n A_i^c \right] \geq \prod_{i = 1}^n(1-x_i) > 0. \end{equation}\]Before proving Lemma 0.7, let us see why it implies Lemma 0.5. Set $x_i = \frac{1}{d+1} < 1$ for all $i$. Then
\(\begin{align} x_i \prod_{\{i,j\} \in E}(1-x_j) &\geq \frac{1}{d+1}\left(1-\frac{1}{d+1}\right)^{\deg(i)}\\ \tag{1} &\geq \frac{1}{d+1}\left(1-\frac{1}{d+1}\right)^{d}\\ \tag{2} &> \frac{1}{(d+1)e} \\ &\geq \mathbb{P}[A_i]. \end{align}\)
- $(1):$ Hypotheses in lemma 0.5 imply that there is a dependency graph $G$ in which each vertex has degree at most $d$.
- $(2):$ The limit definition of exponential is $e^r = \lim_{n \rightarrow \infty} \left(1 + \frac{r}{n}\right)^n$. ◼
It follows by Lemma 0.7 that $\mathbb{P}\left[\bigcap_{i=1}^n A_i^c \right] > 0.$ Now we prove Lemma 0.7.
Proof of Lemma 0.7: Given $S \subseteq [n]$, define
\[P_S:=\mathbb{P}\left[\bigcap_{i \in S}A_i^c\right], ~~~ P_{\emptyset}:=1.\]We want to show, by induction on $|S|$, that $\forall S \subseteq [n]$ and $a\in S$,
\[\tag{†} \frac{P_S}{P_{S\setminus\{a\}}} \geq 1-x_a.\]This indeed yields the result as applying this inequality to $S = [n]$, then $[n-1]$, and so on, we have
\[\mathbb{P}\left[\bigcap_{i = 1}^n A_i^c\right] = P_{[n]} \geq (1-x_n)P_{[n-1]} = (1-x_n)(1-x_{n-1})P_{[n-2]} \geq \cdots \geq \prod_{i = 1}^n(1-x_i) > 0.\]So, it remains to prove $(†)$. In the base case, where $S = \{a\}$, we have
\[\frac{P_{\{a\}}}{P_{\emptyset}} = \mathbb{P}[A_a^c] \geq 1-x_a \prod_{\{a, j\} \in E}(1-x_j) \geq 1 - x_a,\]which proves the base case. Now suppose $(†)$ holds for all $S’ \subseteq [n]$ with size at most $k$ and let $S \subseteq [n]$ have size $k + 1$. In order to make our notation shorter, define the neighbourhood of $a$ and its closure by
\[\Gamma(a) := \{j \in V : \{a, j\} \in E\}, ~~~ \Gamma^+(a) := \\{a\\} \cup \Gamma(a).\]Fix $a \in S$, then
\[\begin{align} P_S & = \mathbb{P}\left[ \bigcap _{i \in S} A_i^c\right]\\ \tag{3} & = \mathbb{P}\left[ \bigcap_{i \in S\setminus \{a\}} A_i^c\right] - \mathbb{P}\left[ A_a \cap \bigcap_{i \in S \setminus \{a\}} A_i^c\right]\\ \tag{4} & \geq \mathbb{P}\left[ \bigcap_{i \in S\setminus \{a\}} A_i^c\right] - \mathbb{P}\left[ A_a \cap \bigcap_{i \in S \setminus \Gamma^+(a)} A_i^c\right]\\ \tag{5} & = P_{S \setminus \{a\}} - \mathbb{P}[A_a]P_{S \setminus \Gamma^+(a)}. \end{align}\]- $(3), (4):$ It becomes clear once you draw a Venn diagram.
- $(5):$ This is because the mutual independence of $A_a$ and $\{A_i : i \notin \Gamma^+(a)\}$.
Dividing $P_{S \setminus \{a\}}$ on both sides ($P_{S \setminus \{a\}}$ > 0 by the induction hypothesis), we have
\[\tag{††} \frac{P_S}{P_{S \setminus \{a\}}} \geq 1 - \mathbb{P}[A_a] \frac{P_{S \setminus \Gamma^+(a)}}{P_{S \setminus \{a\}}}.\]Denote $\Gamma(a) \cap S = \{b_1, …, b_d\}$ where $d \in \mathbb{N}$, and rewrite the fraction on the right hand side as a telescoping product:
\[\frac{P_{S \setminus \Gamma^+(a)}}{P_{S \setminus \{a\}}} = \frac{P_{S \setminus \{a, b_1\} }}{P_{S \setminus \{a\}}} \frac{P_{S \setminus \{a, b_1, b_2\} }}{P_{S \setminus \{a, b_1\}}} \cdots \frac{P_{S \setminus \{a, b_1, ..., b_d\} }}{P_{S \setminus \{a, b_1, ..., b_{d-1}\}}},\]where all the terms on the right hand side are strictly positive by the inductive hypothesis. Also by the inductive hypothesis, each fraction on the right hand side is bounded above by $\frac{1}{1-x_{b_i}}$. Therefore,
\[\frac{P_{S \setminus \Gamma^+(a)}}{P_{S \setminus \{a\}}} \leq \frac{1}{1-x_{b_1}}\cdots \frac{1}{1-x_{b_d}}.\]By the assumption stated in Lemma 0.7, we have $\mathbb{P}[A_a] \leq x_a \prod_{b \in \Gamma(a)} (a-x_b)$, $(††)$ becomes
\[\frac{P_S}{P_{S \setminus \{a\}}} \geq 1-x_a\prod_{b \in \Gamma(a)}(1-x_b) \prod_{c \in \Gamma(a) \cap S} \frac{1}{1-x_c} \geq 1-x_a > 0.\]This proves $(†)$ and completes the proof of Lemma 0.7. ◼